Causal inference with beta regression
In this ninth post of the causal inference + GLM series, we explore the beta likelihood for continuous data restricted within the range of 0 to 1.
In this ninth post of the causal inference + GLM series, we explore the beta likelihood for continuous data restricted within the range of 0 to 1.
In this seventh post of the causal inference series, we apply our approach to ordinal models. Ordinal models make causal inference tricky, and it’s not entirely clear what the causal estimand should even be. We explore two of the estimands that have been proposed in the literature, and I offer a third estimand of my own.
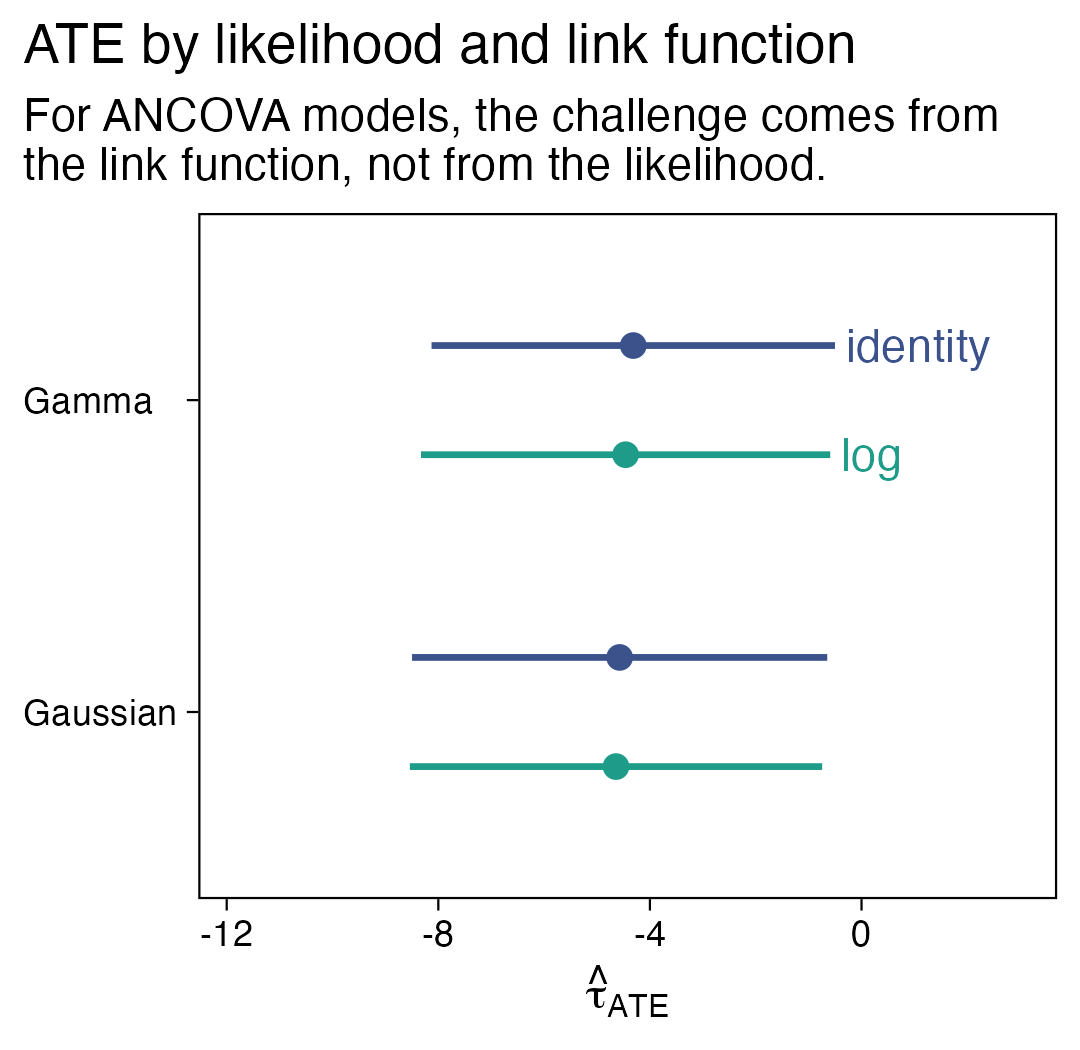
So far the difficulties we have seen with covaraites, causal inference, and the GLM have all been restricted to discrete models (e.g., binomial, Poisson, negative binomial). In this sixth post of the series, we’ll see this issue can extend to models for continuous data, too. As it turns out, it may have less to do with the likelihood function, and more to do with the choice of link function. To highlight the point, we’ll compare Gaussian and gamma models, with both the identity and log links.
In this fifth post of the causal inference series, we practice with Poisson and negative-binomial models for unbounded count data. Since I’m a glutton for punishment, we practice both as frequentists and as Bayesians. You’ll find a little robust sandwich-based standard error talk, too.
In this fourth post, we refit the models from the previous posts with Bayesian software, and show how to compute our primary estimates when working with posterior draws. The content will be very light on theory, and heavy on methods. So if you don’t love that Bayes, you can feel free to skip this one.
In this post, we discuss ways to set a prior for sigma when you know little about your sum-score data. Along the way, we intruduce Popoviciu’s inequality, the uniform distribution, and the beta-binomial distribution.
This is a follow-up to my earlier post, Notes on the Bayesian cumulative probit. This time, the topic we’re addressing is: After you fit a full multilevel Bayesian cumulative probit model of several Likert-type items from a multi-item questionnaire, how can you use the model to compute an effect size in the sum-score metric?
In this post, I have reformatted my personal notes into something of a tutorial on the Bayesian cumulative probit model. Using a single psychometric data set, we explore a variety of models, starting with the simplest single-level thresholds-only model and ending with a conditional multilevel distributional model.
You’re an R user and just fit a nice multilevel model to some grouped data and you’d like to showcase the results in a plot. In your plots, it would be ideal to express the model uncertainty with 95% interval bands. If you’re a frequentist and like using the popular lme4 package, you might be surprised how difficult it is to get those 95% intervals. I recently stumbled upon a solution with the emmeans package, and the purpose of this blog post is to show you how it works.
After tremendous help from Henrik Singmann and Mattan Ben-Shachar, I finally have two (!) workflows for conditional logistic models with brms. These workflows are on track to make it into the next update of my ebook translation of Kruschke’s text. But these models are new to me and I’m not entirely confident I’ve walked them out properly. The goal of this blog post is to present a draft of my workflow, which will eventually make it’s way into Chapter 22 of the ebook.
The purpose of this blog post is to show how one might make ICC and IIC plots for brms IRT models using general-purpose data wrangling steps.
When your MCMC chains look a mess, you might have to manually set your initial values. If you’re a fancy pants, you can use a custom function.
This post is the second of a two-part series. In the first post, we explored how one might compute an effect size for two-group experimental data with only 2 time points. In this second post, we fulfill our goal to show how to generalize this framework to experimental data collected over 3+ time points. The data and overall framework come from Feingold (2009).
I recently came across Jeffrey Walker’s free text, Elements of statistical modeling for experimental biology, which contains a nice chapter on 2-timepoint experimental designs. Inspired by his work, this post aims to explore how one might analyze non-experimental 2-timepoint data within a regression model paradigm.
PhD candidate Huaiyu Liu recently reached out with a question about how to analyze clustered data. Liu’s basic setup was an experiment with four conditions. The dependent variable was binary, where success = 1, fail = 0. Each participant completed multiple trials under each of the four conditions. The catch was Liu wanted to model those four conditions with a multilevel model using the index-variable approach McElreath advocated for in the second edition of his text. Like any good question, this one got my gears turning. Thanks, Liu! The purpose of this post will be to show how to model data like this two different ways.
This is an early draft of my second attempt at explaining the connection between meta-analyses and the Bayesian multilevel model. This time, we focus on odds ratios. Enjoy!
You too can make Kruschke-style model diagrams with the tidyverse and patchwork packages. Here’s how.
When you have a time-varying covariate you’d like to add to a multilevel growth model, it’s important to break that variable into two. One part of the variable will account for within-person variation. The other part will account for between person variation. Keep reading to learn how you might do so when your time-varying covariate is binary.
Binary data are a little weird. In this post, we’ll focus on how to perform power simulations when using the binomial likelihood to model binary counts.
Data analysts need more than the Gauss. In this post, we’ll focus on how to perform power simulations when using the Poisson likelihood to model counts.
When researchers decide on a sample size for an upcoming project, there are more things to consider than null-hypothesis-oriented power. Bayesian researchers might like to frame their concerns in terms of precision. Stick around to learn what and how.
\(H_0\) with simulation.If you’d like to learn how to do Bayesian power calculations using brms, stick around for this multi-part blog series. Here with part I, we’ll set the foundation.
In response to a DM question, here we practice a few different ways you can combine the posterior samples from your Bayesian models into a single plot.
In many instances, partial pooling leads to better estimates than taking simple averages will, a finding sometimes called Stein’s Paradox. In 1977, Efron and Morris published a great paper discussing the phenomenon. In this post, I’ll walk out Efron and Morris’s baseball example and then link it to contemporary Bayesian multilevel models.
There’s more than one way to fit a Bayesian correlation in brms. Here we explore a few.
\(t\))In this post, we’ll show how Student’s t-distribution can produce better correlation estimates when your data have outliers. As is often the case, we’ll do so as Bayesians.
\(t\)-DistributionThe purpose of this post is to demonstrate the advantages of the Student’s t-distribution for regression with outliers, particularly within a Bayesian framework.
You too can make sideways Gaussian density curves within the tidyverse. Here’s how.
This is an early draft of my first attempt at explaining the connection between meta-analyses and the Bayesian multilevel model. Enjoy!
The purpose of this post is to give readers a sense of how I used bookdown to make my first ebooks. I propose there are three fundamental skill sets you need basic fluency in before playing with bookdown: (a) R and R Studio, (b) scripts and R Markdown files, and (c) Git and GitHub.